One-Sided Test

One-Sided Tests (aka One-Tailed Test, Non-Inferiority Test)

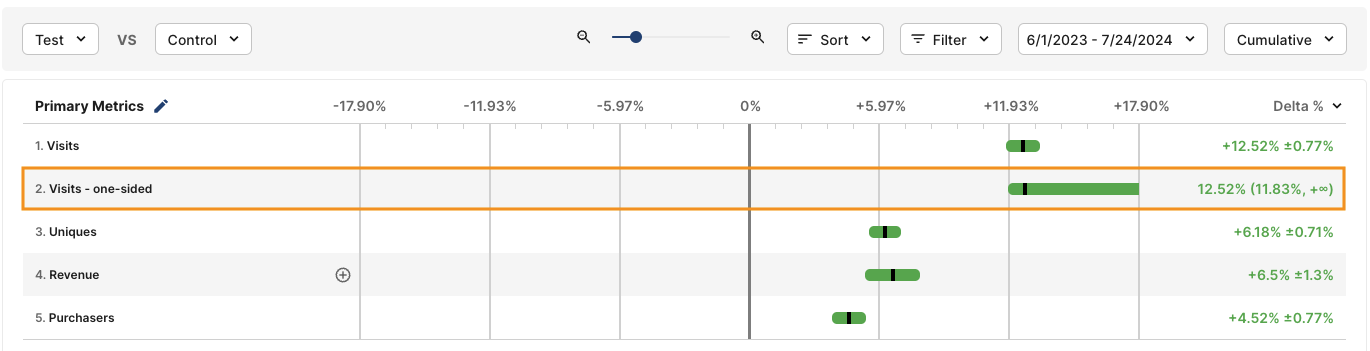
A one-sided test lets you test for a metric moving in only one direction which you specify in advance. This trade off gives you additional sensitivity (or power). It differs from the standard Pulse results which show two-sided results by default.

Use cases for one-sided testing include detecting regressions in guardrail metrics and testing for a change in which only one direction has any meaningful business impact. For example, you may be less interested in detecting if a new feature reduces crash rates, but are very interested in learning if the new feature increases crash rates. In this example, you are willing to forgo detecting the former in favor of better detecting the latter.

One-sided tests completely disregard the possibility of detecting the metric moving in the direction that isn’t specified, but they give you higher sensitivity in the direction you are looking (which allots all your alpha to testing statistical significance in the one direction of interest). This results in one-sided confidence intervals (CIs) that are narrower in the direction of interest than their two-sided counterparts.

How to enable this

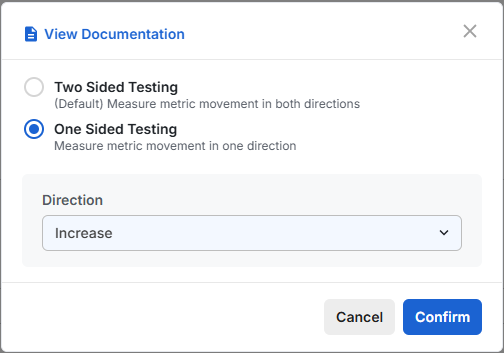
When setting up an experiment and identifying metrics to measure, the default setting is to run a two-sided test. If you want to modify this, simply click on the metric name on the experiment setup screen. This will open a popup where you can modify the test type and indicate a desired direction you seek to measure.

Our V1 doesn’t support Bayesian testing yet.

How to read this

Metrics using one-sided tests will show up in Pulse very similarly to two-sided tests. The only difference will be that we show a one-sided CI rather than a two-sided CI.

Reading one-sided CIs can be a bit confusing at first. They either extend to infinity or negative infinity, which is a bit unusual, but this is entirely expected since we only detect changes in the other direction. As usual with CIs, they indicate that the real mean value of the metric likely falls into this range. Since the CI for the one-sided metric analyzed is so wide, it can be equally useful to read the results as having high confidence the mean value does not fall in the range outside the CI.

FAQ

Why can’t I just run two one-sided tests?

It could be tempting to do this, but in reality it would result in less powerful test. One-sided tests work by allocating the entirety of our Type I error (alpha/significance) to one direction. If we were to add an additional one-sided test in the other direction, we would be re-introducing chance of making a Type I error in that direction. Doing so would mean we claim tighter confidence intervals around metric results that would actually result in higher rates of decision error than the specified confidence level (default: 95%).

Why use a one-sided tests rather than a two-sided test?

This comes down to your use case, metric of interest, and business impact of any decision. Selecting one-sided vs. two-sided tests depends on how you plan to interpret any change in the metric and whether detecting changes in either direction are equally valuable.